 |
ROCKET PROPULSION Supplement #1 |
 |
ROCKET PROPULSION Supplement #1 |
A rocket engine is a device in which propellants are burned in a combustion chamber and the resulting high pressure gases are expanded through a specially shaped nozzle to produce thrust. The function of the nozzle is to convert the chemical-thermal energy generated in the combustion chamber into kinetic energy. The nozzle converts the slow moving, high pressure, high temperature gas in the combustion chamber into high velocity gas of lower pressure and temperature. Gas velocities from 2 to 4.5 kilometers per second can be obtained in rocket nozzles. The nozzles which perform this feat are called DeLaval nozzles (after the inventor) and consist of a convergent and divergent section. The minimum flow area between the convergent and divergent section is called the nozzle throat. The flow area at the end of the divergent section is called the nozzle exit area.
Hot exhaust gases expand in the diverging section of the nozzle. The pressure of these gases will decrease as energy is used to accelerate the gas to high velocity. The nozzle is usually made long enough (or the exit area great enough) such that the pressure in the combustion chamber is reduced at the nozzle exit to the pressure existing outside the nozzle. It is under this condition that thrust is maximum and the nozzle is said to be adapted, also called optimum or correct expansion. To understand this we must examine the basic thrust equation:
F = q × Ve + (Pe - Pa) × Ae
where F = Thrust
q = Propellant mass flow rate
Ve = Velocity of exhaust gases
Pe = Pressure at nozzle exit
Pa = Ambient pressure
Ae = Area of nozzle exit
The product qVe is called the momentum, or velocity, thrust and the product
(Pe-Pa)Ae is called the pressure thrust. As we have seen, Ve and Pe are
inversely proportional, that is, as one increases the other decreases. If a nozzle is
under-extended we have Pe>Pa and Ve is small. For an over-extended nozzle we
have Pe<Pa and Ve is large. Thus, momentum thrust and pressure thrust are
inversely proportional and, as we shall see, maximum thrust occurs when Pe=Pa.
Let us now consider an example. Assume we have a rocket engine equipped with an extendible nozzle. The engine is test fired in an environment with a constant ambient pressure. During the burn, the nozzle is extended from its fully retracted position to its fully extended position. At some point between fully retracted and fully extended Pe=Pa (see figure below).
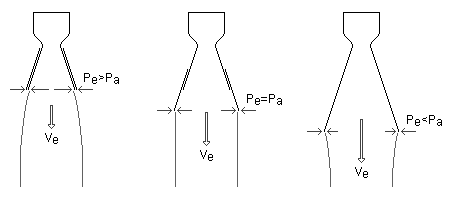
As we extend the nozzle, the momentum thrust increases as Ve increases. At the same time the pressure thrust decreases as Pe decreases. The increase in momentum thrust is greater than the decrease in pressure thrust, thus the total thrust of the engine increases as we approach the condition Pe=Pa. As we continue to extend to nozzle the situation changes slightly. Now the pressure thrust changes in magnitude more rapidly than the momentum thrust, thus the total thrust begins to decrease.
Let's now apply some numbers to our example and run through the calculations to prove that this is true. Assume our rocket engine operates under the following conditions:
q = Propellant mass flow rate = 100 kg/s k = Specific heat ratio = 1.20 M = Exhaust gas molecular weight = 24 Tc = Combustion chamber temperature = 3600 K Pc = Combustion chamber pressure = 5 MPa Pa = Ambient pressure = 0.05 MPa
If the nozzle is properly adapted to the operating conditions we have Pe=Pa, or Pe=0.05 MPa.
The gas pressure and temperature at the nozzle throat is less than in the combustion chamber due to the loss of thermal energy in accelerating the gas to the local speed of sound at the throat. Therefore, we calculate the pressure and temperature at the nozzle throat,
Pt = Pc × [1 + (k - 1) / 2]-k/(k-1) Pt = 5 × [1 + (1.20 - 1) / 2]-1.20/(1.20-1) Pt = 2.82 MPa = 2.82x106 N/m2 Tt = Tc × [1 / (1 + (k - 1) / 2)] Tt = 3,600 × [1 / (1 + (1.20 - 1) / 2)] Tt = 3,273 K
The area at the nozzle throat is given by
At = (q / Pt) × SQRT[ (R' × Tt) / (M × k) ] At = (100 / 2.82x106) × SQRT[ (8,314 × 3,273) / (24 × 1.20) ] At = 0.0345 m2
The hot gases must now be expanded in the diverging section of the nozzle to obtain maximum thrust. The Mach number at the nozzle exit is given by
Nm2 = (2 / (k - 1)) × [(Pc / Pa)(k-1)/k - 1] Nm2 = (2 / (1.20 - 1)) × [(5 / 0.05)(1.20-1)/1.20 - 1] Nm2 = 11.54 Nm = (11.54)1/2 = 3.40
The nozzle exit area corresponding to the exit Mach number is given by
Ae = (At / Nm) × [(1 + (k - 1) / 2 × Nm2)/((k + 1) / 2)](k+1)/(2(k-1)) Ae = (0.0345 / 3.40) × [(1 + (1.20 - 1) / 2 × 11.54)/((1.20 + 1) / 2)](1.20+1)/(2(1.20-1)) Ae = 0.409 m2
The velocity of the exhaust gases at the nozzle exit is given by
Ve = SQRT[ (2 × k / (k - 1)) × (R' × Tc / M) × (1 - (Pe / Pc)(k-1)/k) ] Ve = SQRT[ (2 × 1.20 / (1.20 - 1)) × (8,314 × 3,600 / 24) × (1 - (0.05 / 5)(1.20-1)/1.20) ] Ve = 2,832 m/s
Finally, we calculate the thrust,
F = q × Ve + (Pe - Pa) × Ae F = 100 × 2,832 + (0.05x106 - 0.05x106) × 0.409 F = 283,200 N
Let's now consider what happens when the nozzle is under-extended, that is Pe>Pa. If we assume Pe=Pa × 2, we have
Pe = 0.05 × 2 = 0.10 MPa At = 0.0345 m2 Nm2 = (2 / (1.20 - 1)) × [(5 / 0.10)(1.20-1)/1.20 - 1] Nm2 = 9.19 Nm = (9.19)1/2 = 3.03 Ae = (0.0345 / 3.03) × [(1 + (1.20 - 1) / 2 × 9.19)/((1.20 + 1) / 2)](1.20+1)/(2(1.20-1)) Ae = 0.243 m2 Ve = SQRT[ (2 × 1.20 / (1.20 - 1)) × (8,314 × 3,600 / 24) × (1 - (0.10 / 5)(1.20-1)/1.20) ] Ve = 2,677 m/s F = 100 × 2,677 + (0.10x106 - 0.05x106) × 0.243 F = 279,850 N
Now we consider the over-extended condition, that is Pe<Pa. If we assume Pe=Pa / 2, we have
Pe = 0.05 / 2 = 0.025 MPa At = 0.0345 m2 Nm2 = (2 / (1.20 - 1)) × [(5 / 0.025)(1.20-1)/1.20 - 1] Nm2 = 14.18 Nm = (14.18)1/2 = 3.77 Ae = (0.0345 / 3.77) × [(1 + (1.20 - 1) / 2 × 14.18)/((1.20 + 1) / 2)](1.20+1)/(2(1.20-1)) Ae = 0.696 m2 Ve = SQRT[ (2 × 1.20 / (1.20 - 1)) × (8,314 × 3,600 / 24) × (1 - (0.025 / 5)(1.20-1)/1.20) ] Ve = 2,963 m/s F = 100 × 2,963 + (0.025x106 - 0.05x106) × 0.696 F = 278,900 NWe see that both the under-extended and over-extended nozzles produce thrusts less than that produced when the condition Pe=Pa is satisfied. When we plot a graph of total thrust versus the ratio Pa/Pe we obtain the following:
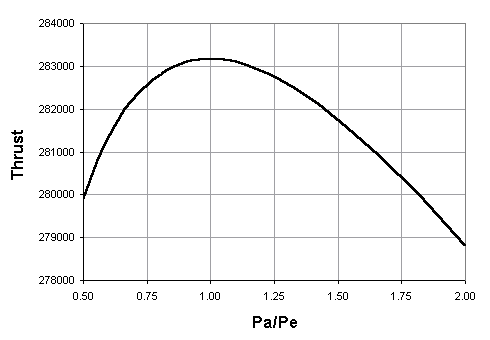
As can be easily seen, thrust is maximum when Pa/Pe=1, or when Pe=Pa.
By Robert A. Braeunig, 1998.